For the hydrogen atom, the energy of the
atomic orbitals depends only on the value of the principal
quantum number, n. This is allowed to take positive integer values
only: n = 1, 2, 3, 4, 5 ....
In the Bohr model, n is directly
related to the radius, r, of the electron's orbit around the
nucleus:
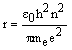
where ε0 =
8.85x10-12
J-1C2m-1 (permittivity of free
space), me = 9.91x10-31 kg (mass of an electron), e =
1.60x10-19 C (charge of a
proton) and h = 6.63x10-34 Js
(Planck's constant).
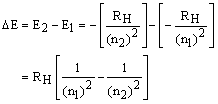
For example, excitation of the electron
from n1 = 1 to n2 = 2, requires:
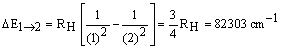
If this energy is provided with light, then
it must be in the ultraviolet region of the spectrum.
Task 2
When an electric discharge is passed through
H2 molecules, they dissociate into excited H atoms. The H
atoms emit light as the excited electron falls down to a lower level
giving rise to a series of emissions, or a spectrum, at different
frequencies.
The lines in the visible region are called the
Balmer lines after their discoverer. The wavenumbers of the Balmer
lines are shown in the table below.
|
wavenumber
of light (cm-1) |
lower
level:
n1 |
upper
level:
n2 |
| |
| |
|
15241 |
|
|
|
20576 |
|
|
|
23045 |
|
|
|
24386 |
|
|
|
25196 |
|
|
|
25720 |
|
|
|
26080 |
|
|
Using the calculator below, complete the table
by trying different values for n1 and n2.
(Hint: all the lines correspond to a common lower level).
Enter the principal quantum number for the lower and upper
level and press 'calculate'. (The answers are presented as powers of
ten: for example 0.1e-01 means 0.1x10-1)
Task 3
The table below lists the wavenumbers for the Lyman
and Paschen series observed in the ultraviolet and infrared
respectively. As for the Balmer series, the lines in each series
correspond to emission from excited levels to a common lower level.
Using the calculator, obtain the lower level involved in both
series.
|
Balmer |
Lyman |
Paschen |
| |
| |
|
15241 |
82303 |
5335 |
|
20576 |
97543 |
7804 |
|
23045 |
102880 |
9145 |
|
24386 |
105350 |
9953 |
|
25196 |
106690 |
10478 |
|
25720 |
107500 |
10838 |
|
26080 |
108020 |
11096 |
| |
|
|
|
lower level: n1 |
lower level:
n1 |
lower level:
n1 |
| |
|
|
Task 4
Use the calculator to work out the ionization energy
for the H atom. This energy can be given as a wavelength (in nm), as
a wavenumber (in cm-1) or as a frequency (in Hz). These
units, although not S.I. units, are commonly used in spectroscopy.
If you want to obtain the answer in S.I. units, use the on-line
converter to convert from these spectroscopic units.
Hint: ionization corresponds to raising the electron
into a very high energy level from the lowest level. Try entering
very large values for n2. Does entering an even higher
value change the answer?
